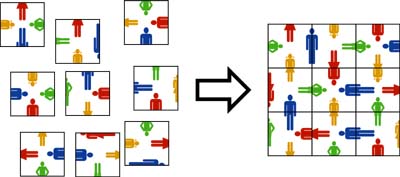
Aus 9 Puzzleteilen soll ein 3x3 großes Quadrat gelegt werden. Auf jedem Puzzleteil sind 4 Symbole zu sehen, die an den Kanten horizontal oder vertikal zerschnitten wurden. Ziel des Spieles ist, die Teile so zusammenzusetzen, dass wieder vollständige Figuren entstehen.
Ein Spiel besteht immer aus 9 Puzzleteilen. Es sorgt dafür, dass alle Puzzleteile gezeichnet werden, indem es den Aufruf von draw() an alle Puzzleteile weiter delegiert. Dabei ordnet es jedem Puzzleteile einen Spritekanal zu. Durch die Methode obenEinsortieren() kann die Tiefensortierung beeinflusst werden. Jedes Puzzleteil, das gezogen oder gedreht wird, wird an die oberste Stelle einsortiert. Die entstehende Lücke wird durch die nachrückenden Puzzleteile wieder aufgefüllt. Die Reihenfolge der Puzzleteile wird durch ihre Position in der Liste mPuzzleteileOrdnung bestimmt, die bei jedem Zeichnen neu ausgewertet wird.
Ein Puzzleteil ist das auf der Spielfläche sichtbare "Kärtchen". Es zeichnet sich durch seine Position und seine aktuelle Drehung aus. Entsprechend definiert es Methoden, um diese Eigenschaften zu manipulieren, nämlich die Methode moveTo(), um das Teil an eine neue Position zu schieben, sowie die Methode rotate(), mit der es um 90 Grad im Uhrzeigersinn gedreht wird. Da es per Klicken und Ziehen mit der Maus auf dem Bildschirm bewegt wird, definiert es außerdem die vom "Drag & Drop"-Objekt benötigten Methoden. Das Puzzleteil repräsentiert die sichtbare Darstellung eines Spielkärtchens auf dem Bildschirm und implementiert folglich die Methode draw(). Es speichert die anzuzeigenden Grafiken allerdings nicht selbst, sondern erbt seine Beschreibung von einem Element-Objekt. Den entsprechenden Grafik-Member für ein Symbol erhält es vom Grafikmanager-Objekt.
Ein Element stellt die logische Einheit des Puzzles dar. Es speichert, in welcher Reihenfolge die Symbole auf den Kärtchen vorkommen und ob diese horizontal oder vertikal durchgeschnitten sind. Es gelten folgende Regeln:
Folglich gibt es für die Symbole nur 6 verschiedene Reihenfolgen:

Jedes Symbol kann in einer von vier Ausrichtungen vorkommen:

Daraus ergeben sich 6 × 4 × 4 × 4 × 4 = 1536 verschiedene Elemente. Ein Element ist durch seine Ordnungsnummer also hinreichend beschrieben. Deshalb hat der new-Handler des Element-Objekt als Argument nur diese Nummer. Aus ihr kann dann bestimmt werden, wie das Element aufgebaut ist. Dabei wird es intern so gehandhabt, dass die Elemente 0-255 die Reihenfolge ABCD in allen möglichen Ausrichtungskombinationen enthalten, Element 256 - 511 die Elemente der Reihenfolge ABDC, u.s.w. Daraufhin werden die 4 Symbol-Objekte konstruiert und gespeichert.
Aufgrund dieser Systematisierung lässt sich jedes Spiel als Liste von 9 Ganzzahlen speichern und in einer Skriptdatei ablegen. Das erste Spiel der Skriptdatei sieht beispielsweise so aus:
[19,235,292,731,404,488,1429,1112,407]
Ein Symbol-Objekt speichert, welches der 4 möglichen Symbole dargestellt wird, und ob es sich um den oberen, unteren, rechten oder linken Teil der Grafik handelt. Welche Grafikdarsteller dies genau sind, ermittelt das Grafikmanager-Objekt. Jede Grafik wird dazu in 4 Teile zerschnitten (oben links, oben rechts, unten links und unten rechts). Der Grafikmanager ermittelt zu einem gegebenen Symbol genau die Grafiken, die zusammengesetzt das richtige Bild ergeben. Als Argument des new-Handlers erhält es dabei eine Liste der zu verwendenden Grafiken aus einer Skriptdatei. Die Symbolgrafik kann im Spiel schnell geändert werden, indem ein Grafikmanager mit einer anderen Liste von Grafiken initialisiert wird. Eine Liste kann zum Beispiel so aussehen:
[[#lo:"sea 1 lo",#ro:"sea 1 ro",#lu:"sea
1 lu",#ru:"sea 1 ru"],
[#lo:"sea 2 lo",#ro:"sea 2 ro",#lu:"sea 2 lu",#ru:"sea
2 ru"],
[#lo:"sea 3 lo",#ro:"sea 3 ro",#lu:"sea 3 lu",#ru:"sea
3 ru"],
[#lo:"sea 4 lo",#ro:"sea 4 ro",#lu:"sea 4 lu",#ru:"sea
4 ru"]]
Das Symbol-Objekt kann mit der Methode istGegenstueck() ermitteln, ob es mit einer gegebenen Symbolhälfte ein vollständiges Symbol ergibt. Ist dies für alle Symbole der Fall, ist das Puzzle gelöst.
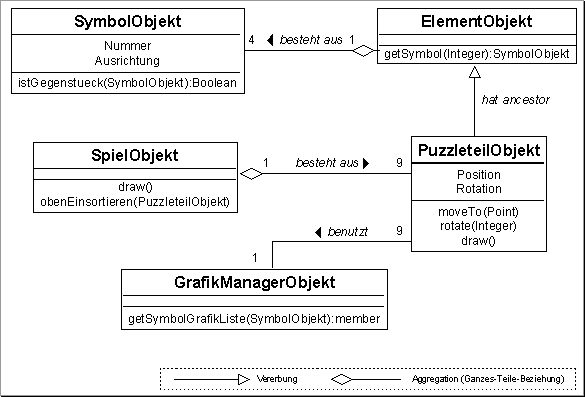
Objektverhältnisse des 3×3-Puzzles
Die Puzzleteile werden vom Benutzer mit der Maus per "Drag & Drop" bewegt. Wird ein Teil nur angeklickt und nicht gezogen, dreht es sich um 90° im Uhrzeigersinn. Ebenso kann die 3×3 Felder große Montagefläche an einer noch nicht belegten Stelle angefasst werden und alle schon zusammengesetzten Puzzleteile auf einmal verschoben werden. Aus diesem Grund habe ich das allgemein gehaltenes "Drag & Drop"-Objekt DragObjekt geschrieben, das für beide Zwecke eingesetzt werden kann.
Der new-Handler des DragObjektes wird mit zwei Argumenten aufgerufen: das erste Argument ist das Objekt, das gezogen werden soll, das zweite ist die Zahl der Pixel, ab denen das Objekt beim Ziehen nicht mehr als angeklickt gelten soll. Durch eine höhere Zahl wird die Klickabfrage toleranter und ein leichtes Abrutschen des Cursors beim Anklicken wird verziehen. Das Ziehen des Objekts wird mit dem Befehl start() eingeleitet. Mit stop() wird das Ziehen beendet und es erfolgt die Auswertung der Aktion. Ein einfacher Aufruf kann z.B. so aussehen:
property mDragObjekt
on mouseDown me
mDragObjekt = script("DragObjekt").new(me, 5) -- 5 Pixel Toleranz
mDragObjekt.start() -- ab jetzt werden die Mausereignisse ausgewertet
end mouseDown
on mouseUp me
if objectP(mDragObjekt) then
mDragObjekt.stop() -- beenden des Ziehens
mDragObjekt = 0 -- Objekt wird nicht mehr benötigt
end if
end mouseUp
Das DragObjekt erwartet vom gezogenen Objekt, dass es folgende Methoden implementiert (Callback-Prinzip):
| on click me | Diese Methode wird nach dem Aufruf der Methode stop() ausgeführt, wenn das Objekt angeklickt wurde, also nicht über dem Toleranzbereich hinausbewegt wurde. |
| on drop me | Diese Methode wird nach dem Aufruf der Methode stop() ausgeführt, wenn das Objekt über den Toleranzbereich hinausgezogen wurde. |
| on startDrag me | Diese Methode wird einmal aufgerufen, sobald das Objekt über den Toleranzbereich hinaus gezogen wurde. |
| on drag me, x, y | Diese Methode wird in jedem Frame aufgerufen, in dem das Objekt gezogen wurde. x und y sind die Koordinaten, an die das Objekt gezogen wurde. |
| on getLoc me | Diese Methode muss die aktuelle Position des Objektes zurückgeben. |
Das letzte Objekt im Puzzle-Programm ist das SpielfeldObjekt. Es speichert die Größe des Spielfelds und welche Puzzleteile an welchen Positionen liegen. Außerdem prüft es, ob das Puzzle gelöst wurde, sobald alle Puzzleteile auf dem Spielfeld liegen. Die Dimensionen des Spielfeldes erfährt das SpielfeldObjekt vom Spielfeld-Verhalten, das auf einem unsichtbaren Darsteller über dem Spielfeld auf der Bühne liegt, welcher auch den aktiven Bereich für Mausklicks über dem Spielfeld darstellt.
| 6 Beispiele | 6.2 Sokoban | ||